Research

Previous Research

A summary of my Doctoral Research:
      Thermal Transport of Nanophononic Crystals

A summary of my Masters Research (pdf):

1. Translating Life Support System Functions into Hardware Requirements and Operational Considerations for a Lunar Outpost Analogue (contact me for further details)
2. Design of a spherical spacecraft: Systems, Management, Structural & Mechanisms (design project)

A summary of my Undergraduate Research (pdf):
      Design Sandwich Composite Deckplates for a Sounding Rocket Application

Overview of my interest in Structural Dynamics

My PhD dissertation focuses on elastic wave propagation in phononic materials at the atomic and continuum levels. The type of phononic materials I have been working on is based on lattice-like periodic configurations in which traveling waves interfere in a manner that provides opportunities for engineering applications. In my research, the focus has been divided into two tracks: (1) the study of elastic wave propagation in periodic beam structures and (2) the study of phonon transport in silicon-based nanophononic crystals. My prime contributions to date are summarized as follows:
• Finite element and transfer matrix analysis of the effects of periodicity truncation in beam structures formed from phononic crystals. This work was verified with experimental vibration testing in which both mechanical shaker and hammer impact testing were conducted along with techniques for FRF data analysis and reduction.
• Development of a Lagrangian formulation for the lattice dynamics of 3D phononic crystals.
• Development of supercell lattice dynamics and thermal conductivity prediction models of silicon-based 3D nanophononic crystals
• Development of supercell models for lattice dynamics calculations and thermal conductivity prediction of silicon thin-films.
Improved knowledge of phonon mechanisms can lead to advances in fundamental material-level concepts such as thermoelectric conversion, thermal shielding (i.e., thermal barrier coatings), and, at larger (µm-m) scales, phononic crystals and acoustic metamateials can be utilized as vibration isolators, acoustic sensors, acoustic lenses, among other applications. It is my goal to continue this work in an environment that allows me to apply these concepts to the aerospace industry.

Natural Frequency: The most fundamental equation of my research is presented below and with just a few variables is something that everyone can understand!

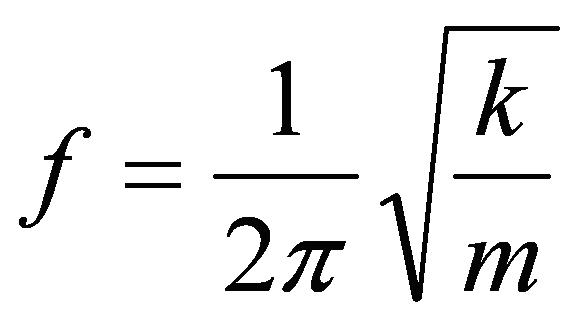
Here f  is the natural frequency of a structure, while k is the stiffness (like the strength of a spring) and m is the mass of a particular structure. The 2*Π term (2*3.14159) simply puts the frequency in units of Hertz [Hz] or cycles per second. To understand this equation, take the example of a structural beam (truss). If you have a beam that is very light and stiff, you will find that your k/m ratio is high and thus you have a high natural frequency. Now if you take the same truss but make it out of a material that is heavier and compliant (less stiff), then your k/m ratio will be much smaller giving a low natural frequency. The k and m values are usually coupled with geometric size where larger systems have lower frequencies and small systems are higher:

Example Values of Fundamental Frequencies: (approximate)

• 0.14 Hz, The Sears Tower
• 0.20 Hz, The Tacoma Narrows Bridge (torsional mode) - Famously collapsed due to vibration instabilities.
• 0.22 Hz, The Golden Gate Bridge (torsional mode) - See note below for Tacoma/Golden Gate Comparison
• 0.9 Hz, The solar array boom on the Mars Reconnaissance Orbiter (a cool spacecraft)
• 1-3 Hz, The suspension system on a car
• 20-40 Hz, A typical automobile frame (smaller cars tend to yield higher frequencies)
• 50-110 Hz, A typical nanosat (100 pound class spacecraft, envelope of 20inch/side, aluminum structure.
• 1000 Hz, A typical wine glass.

*NOTE: The Tacoma bridge collapse was not due to the low natural frequency, but the coupling of this frequency to the aerodynamic flutter of the wind moving over the bridge (they matched at 40mph). You will notice that the Tacoma Narrows bridge had a solid road base which allowed for pressure differentials to build up (like an airplane wing) and induced flutter. Compare this to the Golden Gate Bridge which is porous and allows winds to pass straight through. Other details such as a lack of dampening (energy dissipating joints) played a significant part as well.

Other Neat Analogues: (requires further derivations from fundamental equation shown above)

• A violin instrument, the frequency can be calculated from the string Tension and string density (200 Hz - 3000 Hz)
• A grandfather clock, pendulum frequency can be calculated from the Length of the pendulum and the magnitude of Gravity (designed to 1 Hz)

 
Importance of Natural Frequency:
Every structure has a set of inherent natural frequencies which ideally are only based on the stiffness and mass parameters. An engineer must pick the proper material and geometry to satisfy the vibrational requirements. In a non-ideal world, a new term called dampening is introduced. This is an empirically measured value that characterizes the friction and impurities within the structure and lowers the natural frequencies. Dampening is very important within the physics of vibrations as it enables the amplitude of a vibrating structure to decay over time.

Breaking Stuff with Resonance
When many people hear about resonance at a natural frequency, they think of a wine glass breaking by a high pitched singer, or a bridge collapsing under light winds. This occurs when the input frequency is closely coupled to the structure's natural frequency. When the input frequency is large enough, the inherent dampening in the system does not channel energy away from the vibrating system quickly enough. As a result, the amplitude grows and grows until the k/m ratio changes by destruction.

DANDE Example
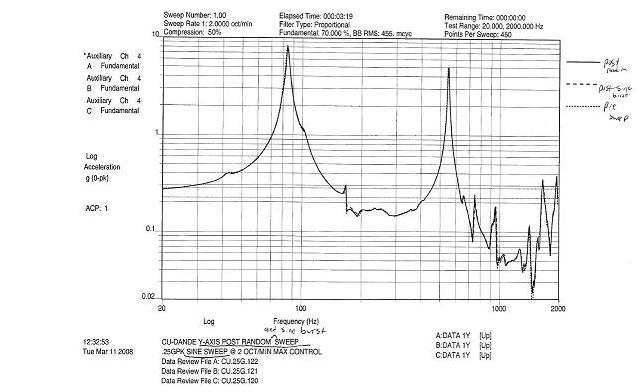
To the right is a picture of the DANDE Spacecraft structural prototype undergoing a vibration test at Ball Aerospace. The result can be seen below which clearly shows the G-forces inside the spacecraft at different frequencies.

This is an example of the frequency response plot of the DANDE spacecraft (found experimentally). A frequency response plot shows how a structural system responds (in terms of g-force on the vertical axis) over a frequency range (horizontal axis). The first and second fundamental frequencies (84 Hz & 540 Hz) can clearly be seen. It is interesting to see how the g-force increases as the input frequency approaches the natural frequency. The reason that DANDE did not break when the shaker table input matched the satellite's natural frequency is due to structural dampening and g-force limiters imparted by the test conductors (me).

Creating Bandgaps in Simple Structures
To demonstrate the ability to create and control band gaps, I have calculated the frequency response plots of a simple six mass-spring chain. From here, I introduced a periodic condition where certain masses are made a bit heavier. The plot below shows the mass chain system in both the normal (red) and modified (blue) states. It is amazing to see how a specific frequency range is created and can be controlled based on the needs of the designer.

My research uses this principle and applies it to large multi-degree-of-freedom systems to simulate wave dispersion through materials.