You are hereThesis
Thesis
Thesis Title:
LATTICE DYNAMICS AND THERMAL TRANSPORT PROPERTIES OF NANOPHONONIC MATERIALS
Motivation
Whether concentric impressions expanding in a pond by a tossed pebble or the vibrations of discrete atoms in a solid subjected to a temperature gradient; similar physical principles can be used to model wave propagation in a medium. The mathematical study of wave propagation dates back to the time of Sir Isaac Newton (1686) where simplistic models were used to determine the speed of sound in air. Today, rigorous mathematical formulations are employed to accurately model the motion of waves in solids, fluids and gases. In the area of solids, research continues to emerge on the elucidation of complex phenomena in non-isotropic elastic media. Aided by increasing computational resources and advanced practices in material processing and structural fabrication, interest in elastic wave propagation studies - especially towards the goals of directing, inhibiting and harvesting energy - is a rich and rapidly expanding field. The study of elastic wave propagation in a solid medium involves a diverse background of mathematics, physics, engineering and material science.
The work presented here focuses on phononic crystals (PnC) or synthetic materials that by nature of their spatial periodicity exhibit unique properties of wave propagation. At the macro scale (μm-m) the elastic motion of PnCs leads to applications such as vibration isolators, acoustic metamaterials and acoustic lenses. In this work however, we focus on the nanoscale where the wavelengths of the propagating waves are on the order of the atomic spacing of a crystalline material and hence influence its thermal transport properties. Improved knowledge of phonon mechanisms can lead to advances in fundamental material-level technologies such as thermoelectric conversion, thermal shielding (e.g., thermal barrier coatings) and thermal waveguides.

For nanostructured devices, the dynamics (i.e. elastic wave propagation) of the structure is commonly modeled as a solid. However for devices this small, we need to instead model the waves atomistically. This is one of the main contributions of my work. (AIP Advances, Davis and Hussein 2011)
There are significant differences between a material and a structure (Hussein 2006). A structure is comprised of one or more materials, its characteristics are dependent on its boundary conditions, and admit to the application of external loads. All these factors have a diverse effect on the dynamical response. A material on the other hand is infinite in extent and is generally viewed at a local level. Here the wave propagation responds to the basic intrinsic features (elasticity, density) of the material forming unique dispersive behavior. This effect can be assessed through a dispersion relationship which compares the temporal frequency with the spatial wavenumber (or wave vector) of the vibrational modes propagating in the medium. In addition, the dispersion relation provides the group and phase velocities of the traveling waves.
At the nanoscale, elastic waves propagating in a crystalline material are on the order of the atomic spacing. This provides an opportunity to construct a new periodic structure, on top of the original periodic structure, and as such realize the concept of a nanophonoic crystal (nanoPnC). The nanoPnCs considered in this work - consist of voided unit cells. As a result, the periodicity is geometrically induced by removing clusters of atoms. Although in many cases a band gap may not form by simply removing material, the shifting in the phonon frequencies and the flattening of the dispersion bands have significant effects on the phonon wave propagation characteristics, leading to changes in the thermal transport properties (when compared to the original baseline crystalline material).
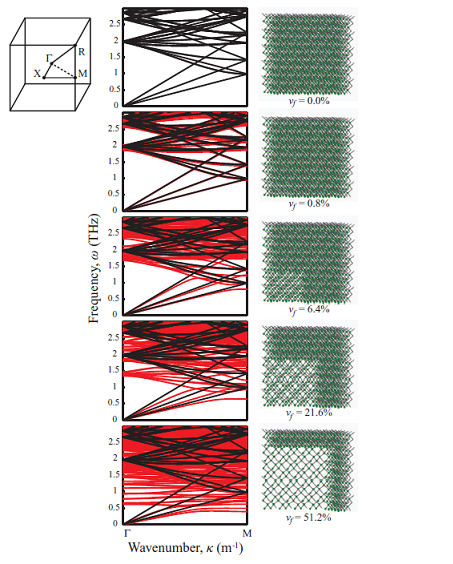
As an example, modeled is a cube of silicon containing 1000 atoms. The top plot shows the bulk (or default crystal) dispersion in black. Dispersion essentially tells us what waves are allowed to propagate in the crystal which is dependent on frequency [units of 1/s] (y-axis) and spatial length (x-axis) [units of 1/m]. This figure shows that when we insert a hole to create a phononic crystal, the dispersion changes dramatically (red), here, vf is equal to the percentage of atoms removed. My work determines the reduction in thermal conductivity of these nanophononic crystals. (AIP Advances, Davis and Hussein 2011)
Outlook
My work models the wave propagation in a series of crystalline structures with the goal to accurately predict the reduction in thermal conductivity. My dissertation goes into future details regarding the effects of void boundaries, truncation and defects on PnCs. Improvements to the thermal efficiency of silicon based devices have the potential to revolutionize the industry across a wide field, including heat dissipation in semiconductors and enhanced thermoelectrics. Within the aerospace industry, there are countless applications to efficient and solid state thermal management devices.
Relevant Publications:
Peer Reviewed Journals
- Davis, B.L., Hussein, M.I., “Thermal characterization of nanoscale phononic crystals using supercell lattice dynamics", AIP Advances 1, 041701 (2011)
- Reinke, C.M., Mehmet F.S., Davis, B.L., Hussein, M.I., Bongsang, K., Hussein, M.I., Olsson-III, R.H., El-Kady, I., “Thermal conductivity prediction of nanoscale phononic crystal slabs using a hybrid lattice dynamics-continuum mechanics technique", AIP Advances 1, 041403 (2011)
Conference Proceedings (Full Papers)
- Davis, B.L.*, Tomchek, A.S., Flores, E.A., Liu, L. and Hussein, M.I., “Analysis of periodicity termination in phononic crystals” Proceedings of 2011 ASME International Mechanical Engineering Congress and R&D Expo, IMECE2011-65666, [CD ROM: pp. 1- 5], Denver, Colorado, 11-17 November 2011.
- Davis, B.L. and Hussein, M.I., “A three-dimensional lumped parameter model of nanoscale phononic crystals,” Proceedings of 22nd ASME Biennial Conference on Mechanical Vibration and Noise, [CD ROM: pp. 1-6], San Diego, California, 30 August - 2 September 2009.
- Hussein, M.I., Ruzzene, M., Leamy, L.J., Durrie, J.J., Davis, B.L., “NEMS Components Design Using Intentionally Defected Dispersive Building Blocks”, ASME International Mechanical Engineering Congress & Exposition, [CD ROM: pp. 1-7], Boston, Massachusetts, 2008.
Conference Proceedings (Extended Abstracts)
- Davis, B.L. and Hussein, M.I., “Thermal transport analysis of silicon-based nanoscale phononic crystals” Proceedings of 2012 ASME 3rd Micro/Nanoscale Heat & Mass Transfer International Conference, Atlanta, Georgia, 3 ̶ 6 March 2012.
- Davis, B.L. and Hussein, M.I., “Thermal transport studies of silicon-based phononic-crystal thin films,” 2011 ASME International Mechanical Engineering Congress and R&D Expo, Denver, Colorado, 11-17 November 2011.
- Tomchek, A.S., Flores, E.A, Liu, L., Davis, B.L. and Hussein, M.I. “Characterization of band gap resonances in finite periodic structures,” Proceedings of Phononics 2011, Paper PHONONICS-2011-0177, pp. 192-13, Santa Fe, New Mexico, USA, May 29-June 2, 2011.
- Davis, B.L. and Hussein, M.I. “Reduction of thermal conductivity in silicon slabs by unit cell nanostructuring,” Proceedings of Phononics 2011, Paper PHONONICS-2011-0174, pp. 236-237, Santa Fe, New Mexico, USA, May 29-June 2, 2011.
- Davis, B.L. and Hussein, M.I., “A building block approach to controlling phonon dynamics in nanostructures: Lattice dynamics in a Lagrangian framework,” Proceedings of the National Science Foundation CMMI Research and Innovation Conference, [Poster Presentation], Atlanta, Georgia, 4 ̶ 7 January 2011.
- Liu, L., Davis, B.L., Tomchek, A.S., Flores, E.A. and Hussein, M.I., “Band gap maps for flexural beams: Effects of periodicity type, properties and termination,” 2010 ASME International Mechanical Engineering Congress and R&D Expo, Vancouver, British Columbia, Canada, 12-19 November 2010.
- Hussein, M.I. and Davis, B.L., “Bloch modal analysis in lattice dynamics: Orders of magnitude reduction in model size,” Workshop on Thermal Transport at the Nanoscale, Telluride, Colorado, 21-25 June 2010.